
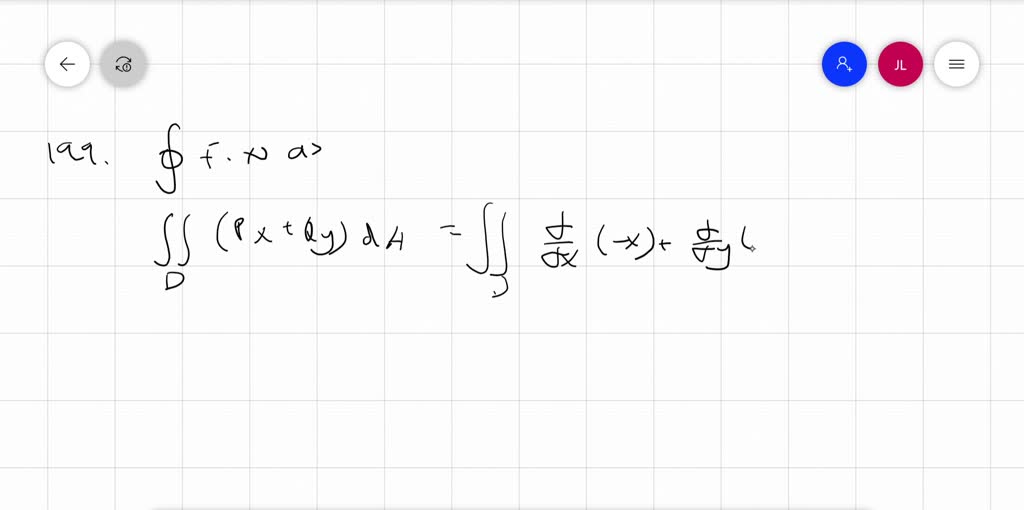
the parametrization, whether clockwise or counterclockwise, does not matter. Summary Stokes theorem is the 3D version of Greens theorem. This surface is the boundary of a three-dimensional volume. What I wanted to check is that the value of the flux integral does not change as long as you are consistent with the choice of unit normal that you use on each piece of the curve (outward or inward), i.e. R_\theta=(-a\sin\theta\sin\phi,a\cos\theta\sin\phi, 0),\ \ \ r_\phi=(a\cos\theta\cos\phi, a\sin\theta\cos\phi, -a\sin\phi). If you think back to chopping up the surface to get many tiny little line integrals, this basically says all those little line integrals cancel out with nothing left to show for their work. The "first octant" is chosen by the region where we let $\theta$ and $\phi$ vary (if you think carefully about it you'll see that $\pi/2$ is the right choice above). In this case, since S is a sphere, you can use spherical. This form of Green’s theorem allows us to translate a difficult flux integral into a double integral that is often easier to calculate. The flux of a fluid across a curve can be difficult to calculate using the flux line integral. S F n d S D F ( r ( s, t)) ( r s × r t) d s d t, where the double integral on the right is calculated on the domain D of the parametrization r. The flux form of Green’s theorem relates a double integral over region D to the flux across boundary C.

R(\theta, \phi)=(a\cos\theta\sin\phi, a\sin\theta\sin\phi, a\cos\phi),\ \ 0\leq\theta\leq\frac\pi2,\ \ 0\leq\phi\leq\frac\pi2. The way you calculate the flux of F across the surface S is by using a parametrization r ( s, t) of S and then. In this case, since $S$ is a sphere, you can use spherical coordinates and get the parametrization To find the outward flux of vector field F (x2 + y2)i + (x - y)j across the closed curve C, we can apply Greens Theorem, which states that the outward. Where the double integral on the right is calculated on the domain $D$ of the parametrization $r$. This means the net outward flux of the electric field lines normal to the surface enclosing the charge is equal to the. Use the divergence theorem to find the outward flux of F(x, y. Now, lets look at the Gausss law in electrostatics: In differential form, it reads. Arguing as before, we get z f(x, y)4 - 2x - y, hence also. We’ll find that flux integrals require a few extra steps in addition to those above to make them easier. ( Given that vector n points outwards of the area around the ice cube and the fire.) Comment. For instant calculating the heat flux around an ice cube, where you would get a negative flux or around a fire where you would get a positive flux. That, therefore, is what I want to focus on tonight. Absolutely not Actually you see this in tasks a lot. In that case, the direction of the normal vector at any point on the surface points from the inside to the outside.The way you calculate the flux of $F$ across the surface $S$ is by using a parametrization $r(s,t)$ of $S$ and then Intuitively, it states that the sum of all sources minus the sum of all sinks gives the net flow out of a region. Of all the kinds of surface integrals you’ll encounter, I think the hardest has flux integrals, because the concept of flux is something that a lot of people have trouble understanding. However, if a surface is closed, then the surface encloses a volume. (c) Only \(S_3\) has been given a consistent set of normal vectors that allows us to define the flux through the surface.

(b) The outward normal is used to calculate the flux through a closed surface. \): (a) Two potential normal vectors arise at every point on a surface.


 0 kommentar(er)
0 kommentar(er)
